SocioDone

Вычисляем предельную ошибку выборки ε=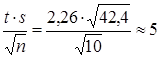(кг).

Доверительный интервал для генеральной средней:

327—5<<327+5 или 322<<332.

Пример 1.9.8.Используя данные примера 1.9.7, определить объем выборки, необходимый для того, чтобы ошибка выборочной средней с вероятностью 0,95 не превышала 3 рубля.

Решение.

Мы имеем оценку генеральной дисперсии s2 = 42,4. Вначале находим n1 по формуле (1.9.25), принимая σ2 = s2 и определяя z по таблице функции Лапласа:

Теперь обращаемся к таблице функции Стьюдента и по Р = 0,95,

v1 = n1—1 ≈ 17 находим значение t1=2,11.

Вычисляем

По Р = 0,95 и v2 = n2—1 = 21 – 1 = 20 находим t2 = 2,09.

Вычисляем

Поскольку n3 ≈ n2 , то необходимый объем выборки устанавливается 21 человек.

Еще раз отметим, что рассмотренные выше схемы решения задач для малых выборок справедливы только при предположении нормального характера генерального распределения. При отсутствии такого предположения распределения неизвестно, и выборочную среднюю можно использовать лишь как точечную оценку генеральной средней без оценки точности .приближенного равенства , т. е. без расчета доверительного интервала.

Другие материалы:

Постиндустриальный проект и действительность
Однако общемировая ситуация развивается во многом по другому сценарию. В ней проступают тенденции и черты, которые внушают все меньше оптимизма и, более того, - вызывают опасения. Причем эти тенденции прямо или косвенно связаны с новыми п ...

Младший школьный возраст
У младших школьников, воспитанников учреждений интернатного типа, обнаружены специфические отклонения в развитии интеллектуальной и мотивационно - потребностной сфер психики. Они проявляются, в частности, в задержках развития внутреннего ...

Причины возникновения неполной семьи в современном обществе
Вопрос о неполных семьях актуален потому, что в них сосредоточена значительная часть того населения, у которого не сложились естественные, заложенные в самой природе семейно-брачных отношений условия жизни. Это дети, без отца (или матери) ...