SocioDone

Если генеральная совокупность подчинена нормальному закону распределения (что на практике имеет место очень часто), то выборочная средняя как средняя арифметическая п нормально распределенных случайных величин также имеет нормальный закон распределения. Таким образом, величина 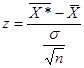распределена по стандартному нормальному закону, и схема решения задач при известном генеральном среднем квадратическом отклонении σ остается прежней.

Если же генеральное среднее квадратическое отклонение σ неизвестно и приходится пользоваться его выборочной оценкой s, то используется статистика t (1.9.26), которая, как мы уже отмечали, подчинена закону распределения Стьюдента с v = n—1 степенями свободы. При v < 30 имеются значительные различия между распределением Стьюдента и нормальным распределением (тем более значительные, чем меньше v). Используя функцию распределения Стьюдента, мы можем записать равенство, аналогичное формуле Лапласа:

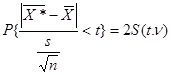(1.9.27)

где S(t, v) — функция Стьюдента, значения которой для различных значений t

и v подробно рассчитаны и представлены в специальных таблицах.

Выражение (

1.9.27)

эквивалентно выражению:

(1.9.28)

где

Решение задач с помощью этого равенства аналогично решению задач с использованием формулы Лапласа. Лишь определение п несколько усложняется из-за того, что оно входит также в параметр v = n—1.

Поэтому можно воспользоваться схемой последовательных приближений. Вначале производят оценку (s2) генеральной дисперсии. Затем находят п1 по схеме (1.9.25), используя таблицу функции Лапласа и принимая σ2 = s2- По найденному n1 и, соответственно, v1 = n1 — 1 и заданному значению

Р=1—α определяют t1 (по таблице распределения Стьюдента) и вычисляют и так далее.

Теперь можно снова повторить расчет по v2 = n2 — 1 и т.д.

Итерация заканчивается, если окажется ni ≈ ni-1.

Пример 1.9.7.

Для определения среднего заработка работника за день при соблюдении необходимых условий было отобрано 10 работников, заработок которых оказался равным (в руб.): 325; 337; 319; 330; 327; 328; 332; 320; 318; 334. Требуется определить с вероятностью 0,95 доверительный интервал для среднего заработка работников в генеральной совокупности, если есть основания полагать, что заработная плата в генеральной совокупности подчиняется нормальному закону определения.

Решение:

По данным выборки определяем среднюю и дисперсию. Получаем

;

Рассчитываем несмещенную оценку генеральной дисперсии

Предположение о нормальном характере генерального распределения позволяет нам использовать равенства (1.9.27) и (1.9.28). Обращаясь к таблице значений функции Стьюдента, по заданным P = 2S(t, v)=0,95 и v = n—1 = 10 – 1 = 9 находим t = 2,26.

Другие материалы:

Классификация гипотез в программе социологического исследования
При отсутствии четких гипотез, когда исследование проводится по фомлулятивному (примерному) плану, применяют простое или бесструктурное наблюдение. Цель такого предварительного наблюдения заключается в том, чтобы придумать гипотезы для бо ...

Методы социальной диагностики.
Кроме описанных методов диагностирования личности следует выделить следующие. Наблюдение — метод, который используется при изучении внешних проявлений поведения человека, по которым можно составить представление о нем. Существуют различн ...

Социальные основы действия работников
Каковы же мотивы, которые движут исполнителями в коллективных действиях? Ортодоксальные марксисты в любой забастовке видят в первую очередь проявление коллективной солидарности рабочего класса, свидетельство его «коллективной рациональнос ...