SocioDone

Для точечной оценки доли признака в генеральной совокупности (р) естественно взять выборочную долю

р*=

где n — объем выборки,

т — количество единиц в выборке, обладающих данным признаком.

Можно доказать, что эта оценка является состоятельной, несмещенной, эффективной.

Вопрос об интервальной оценке рассмотрим сначала для случая возвратной выборки.

При такой организации выборки случайная величина p*, как известно из теории вероятностей, имеет биномиальный закон распределения. Расчет доверительного интервала с применением формулы биномиального закона связан с определенными вычислительными трудностями. Однако при достаточно большом объеме выборки (примерно n ≥ 20, пр ≥ 10) биномиальное распределение хорошо аппроксимируется нормальным распределением с параметрами

М (p*) = p;

σ(p*) =

Следовательно, случайная величина имеет стандартное нормальное распределение (с параметрами M(z)=0; σ(z)=1).

Задавшись определенной вероятностью Р=1— α, имеем:

2Ф

(zα)=1- α (1.9.7)

где Ф

(zα)=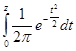 — интегральная функция Лапласа, значения которой для различных значений z рассчитаны и приводятся в специальных таблицах.

Равенство (1.9.7) эквивалентно равенству:

P {│p*- p │<z1 · σ( p*)} = 2Ф

(zα) (1.9.7')

Таким образом, предельная ошибка выборки εα определяется из равенства:

(1.9.8)

Применение этой формулы затрудняется тем, что в нее входит неизвестный параметр р — генеральная доля. Однако при большом п можно заменить неизвестный параметр р его точечной оценкой р*. Тогда получим:

(1.9.9)

Приведенные выше формулы связывают между собой, в конечном счете, три величины: доверительную вероятность Р=1−α, предельную ошибку выборки ε и объем выборки п.

В каждой конкретной задаче две из этих величин задаются и определяется третья величина. Таким образом, мы имеем следующие три типа задач:

I. Даны п и Р, определить ε.

II. Даны п и ε, определить Р.

III. Даны Р и ε, определить п

Первые два типа задач связаны с анализом результатов уже произведенной выборки объема п, следовательно, и с найденной точечной оценкой р*.

Задачи третьего типа должны решаться до проведения выборки. По заданной доверительной вероятности P мы можем определить величину z (по таблице интегральной функции Лапласа). Из (1.9.9) получаем:

(1.9.10)

Но в (1.9.10) входит величина р*, получаемая в результате выборки, а речь идет об определении п до осуществления выборки.

Поскольку р* неизвестно, то определяем из этого равенства, при каком значении р* величина п будет максимальной. Используя обычный метод следования функции на максимум, получаем:

откуда р*=½

Следовательно,

(1.9.11)

Выборка такого объема наверняка обеспечит заданные надежность и точность.

Рассмотрим примеры на каждый из трех типов задач. Исследуется вопрос о доле поврежденных клубней картофеля после механической уборки.

Другие материалы:

Проблемы девиантного поведения на предприятиях
Одна из наиболее негативных тенденций развития цивилизации состоит в постоянном росте преступности, в том числе на рабочем месте. Воровство, взятки, мошенничество, коррупция, уклонение от уплаты налогов, искажение данных бухгалтерского у ...

Базовые принципы
Эффективность и надежность прогнозов предопределяется многими факторами, в том числе и соблюдением основных принципов подхода и самого процесса исследования. К числу важнейших из них относятся: - выбор основных факторов и элементов данн ...

Точечные оценки для средней и дисперсии генеральной совокупности
Обозначим через и σ2 среднюю и дисперсию генеральной совокупности. Возвратная выборка объема n может рассматриваться как совокупность n независимых случайных величин Xj, имеющих одно и то же распределение, совпадающее с генеральным ...