SocioDone

Пример 1.9.1Произведена случайная выборка объемом.n=200 деталей. Из них поврежденных оказалось 40. Определить с вероятностью 0,95 доверительный интервал для доли поврежденных деталей генеральной совокупности.

Рассчитываем выборочную долю:

р* = m / n = 40 / 200 = 0.20

По заданной доверительной вероятности

Р = 1 – α = 2Ф

(zα) = 0.95

находим по таблице интегральной функции Лапласа соответствующее значение zα =1,96. Применяем формулу (1.9.9):

Таким образом, доверительный интервал для генеральном доли р:

0,20-0,06<p<0,20+0,06, или 0,14<p<0,26

Пример 1.9.2.

По результатам той же выборки определить вероятность того, что ошибка выборки не превысит 0,03.

Имеем:

Отсюда:

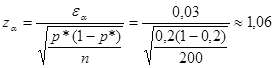
По таблице интегральной функции Лапласа находим соответствующую доверительную вероятность Р = 2Ф

(zа )=0,71.

Пример 1.9.3.До проведения выборки необходимо ответить на вопрос: какой объем выборки обеспечит с вероятностью

0,95 ошибку выборзки не более, чем 0,02?

Применяем формулу (1.9.11):

Следует заметить, что требуемые надежность и точность может обеспечить в нашей задаче и выборка меньшего объема.

Если до проведения выборки

у нас есть приближенная оценка хотя бы максимальной величины р*, то мы

можем применить формулу (1.9.10) и получить меньшее значение необходимого объема выборки п.

В случае безвозвратной выборки случайная величина р*, как доказывается

в теории вероятностей, имеет так называемое гипергеометрическое распределение. Ее математическое ожидание,

как и в случае возвратной

выборки, равно генеральной доле: М(р*)=р, а среднее квадратическое

отклонение вычисляется но формуле:

(1.9.12)

где N — объем генеральной совокупности

При

достаточно большом объеме выборки гипергеометрическое

распределение также хорошо аппроксимируется

нормальным распределением с указанными параметрами M(p*) и σ(p*), поэтому дальнейший ход решения задач аналогичен рассмотренному выше случаю возвратной выборки.

Формула для предельной выборки принимает вид

(1.9.13)

При решении задач III типа из (1.9.13) получаем:

(1.9.14)

Соответственно изменится и формула для nmax :

(1.9.15)

Если объем выборочной совокупности n составляет незначительную долю по отношению к объему генеральной совокупности N, то величина в формуле (1.9.12) ближе к 1, можно пренебречь различием формул (1.9.9) и (1.9.13) и пользоваться более простыми соотношениями для возвратной выборки, даже если фактически выборка производится как безвозвратная.

В заключение раздела необходимо отметить что в статистике используется понятие средней ошибки выборки, которая определяется как среднее квадратическое отклонение соответствующей выборочной характеристики. Нетрудно видеть, что формула для средней ошибки выборки является частным случаем формулы предельной ошибки выборки при z=1.

Другие материалы:

Религия, ее место в системе отношений человека и окружающего мира. Атеизм
Религия является одной из древнейших и основных (наряду с наукой, образованием, культурой) форм духовной культуры. В современной науке популярно определение религии, исходящее из признания ее основой веры в Бога («религия есть вера в Бога ...

Демографическая политика Казахстана и социологическое развитие семьи
Демографическая политика составляет основу внутренней политики любого подлинного независимого государства. Для одних является актуальной угроза перенаселения (Китай, Индия, Египет и др.), для других - недонаселенность (Австралия, Канада, ...

Международные и российские нормативные, правовые документы в области защиты прав женщин и детей
Насилие по отношению к женщине отражает ситуацию в обществе в целом, является своеобразным социальным индикатором. Основным социальным противоречием является то, что женщины, как правило, не знают своих законных прав и, соответственно, не ...