SocioDone

Если объем выборки достаточно большой (практически, начиная с п > 20—30), то распределение выборочной средней , согласно центральной предельной теореме, независимо от характера генерального распределения приближается к нормальному распределению с параметрами

М()= и )

где — генеральная средняя,

σ— генеральное среднее квадратическое отклонение,

п — объем выборки.

Таким образом, величина

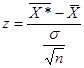
распределена по стандартному нормальному закону (с математическим ожиданием M(z) = 0 и средним квадратическим отклонением σ(z) = 1).

Задавшись доверительной вероятностью Р = 1 — α, определяем из равенства 2Ф(z) = 1 — α соответствующее значение za (используем при этом таблицу интегральной функции Лапласа). Тогда с вероятностью Р = 1 — α выполняется неравенство:

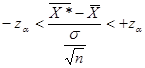(1.9.22)

которое эквивалентно неравенству:

(1.9.23)

Величина называется предельной ошибкой выборки.

Таким образом, мы имеем доверительный интервал для генеральной средней:

( ; )

Наоборот, если задана предельная ошибка ε , а требуется определить вероятность Р, то схема решения задачи следующая:

ε→z=→Ф(z)→P=2Ф(z) (1.9.24)

Наконец, определение объема выборки п по данным Р и ε производится по следующей схеме:

P=2Ф(z) →z→n= (1.9.25)

Пример 1.9.4.

Взвешивание 50 случайно отобранных коробок печенья дало =1200г. Определить с вероятностью Р = 0,95 доверительные границы для среднего веса коробки печенья в генеральной совокупности, если есть основания полагать, что генеральная дисперсия σ2 = 11664.

Решение:

Дано: n=50; =1200; σ2 =11664 (= 108); Р = 0,95.

Из равенства Р = 2Ф(z)=0,95 по таблице значений интегральной функции Лапласа находим z=1,96, откуда:

ε=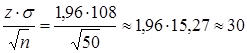(г)

Таким образом, получаем доверительный интервал:

1200 — 30 < < 1200 + 30.

Пример 1.9.5Определить, с какой доверительной вероятностью можно утверждать, что при данном объеме выборки (50 коробок) ошибка выборки не превысит 20 г.

Решение:

По величине ε=20 вычисляем , откуда по таблице Ф(z): Р = 2Ф(1,31)≈0,81

Пример 1.9.6.Определить необходимый объем выборки n, который с вероятностью 0,99 гарантировал бы ошибку выборки не более чем ε = 20 г.

Решение:

Из Р = 2Ф(z) =0,99 находим z = 2,58, откуда:

Другие материалы:

Социологическое развитие семьи
Динамику социального развития семьи в Казахстане, можно проследить по статье Алимбековой Г.Т., кандидата социологических наук; ЦИОМ, Алматы, Казахстан. В данной статье представлены результаты исследования состояния современной казахстанс ...

Фактический брак.
Фактическим браком именуются отношения между состоящими в них лицами, удовлетворяющие всем требованиям и условиям вступления в брак, но не зарегистрированные в установленном законом порядке. Фактический брак не может породить тех. правовы ...

Анализ рядов динамики
Важной задачей статистики является изучение явления во времени. Для решения этой задачи необходимо иметь данные по определенному кругу показателей на ряд моментов времени, следующих друг за другом. Ряд расположенных в хронологической пос ...