SocioDone

Одна из важных задач математической статистики заключается в том, чтобы по данным случайной выборки оценить достаточно точно значения характеристик генерального распределения, как, например, долю признака, среднюю, дисперсию и т. д. Задачу об оценке можно разделить на две части: какую величину, подсчитанную по выборке, принять в качестве приближенного значения характеристики генерального распределения (точечная оценка), и в каком интервале вокруг этой величины будет заключена с заданной надежностью искомая характеристика (интервальная оценка).

Пусть генеральное распределение задается некоторой функцией F(x,ξ1,…,ξк), где ξ1,…,ξк - его параметры. Например, если распределение задается двумя параметрами ξ1 и ξ2, то ξ1 обычно характеризует среднюю, а ξ2- дисперсию (или среднее квадратическое отклонение) генерального распределения.

Случайный отбор позволяет выборку объема п рассматривать как п повторных испытаний. Результат каждого испытания (j-го единичного отбора) есть случайная величина Хj, а вся выборка — совокупность п случайных величин {Х1, … Хj, ., Хп} Любая конкретная выборка (х1, ., хi, ., хп) есть реализация этой совокупности случайных величин.

Для оценки неизвестного параметра ξ генеральной совокупности введем некоторую величину θ, вычисляемую по результатам выборки, т. е.

θ = θ (X1, ., Хj, ., Хп),

называемую статистикой.

Так, если для оценки генеральной средней ξ = выбрана статистика θ = Х* — выборочная средняя, то ее значения могут быть подсчитаны по результатам выборки как

Если для оценки генеральной дисперсии D выбрана статистика θ =D* — выборочная дисперсия, то ее значения могут быть рассчитаны по формуле

Статистика θ есть случайная величина. В ряде случаев можно найти ее распределение.

Статистическая оценка должна быть возможно более точной. С этой целью к статистике θ предъявляются требования:

1) состоятельности,

2) несмещенности,

3) эффективности.

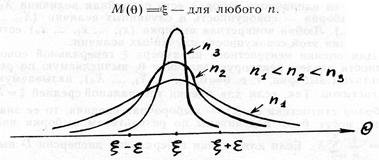
1) Свойство состоятельности означает, что распределение статистики θ с ростом объема выборки п концентрируется в сколь угодно малое окрестности параметра ξ (статистика θ стремится по вероятности к оцениваемому параметру ξ). Свойство состоятельности выражается предельным равенством: для любого столь угодно малого положительного числа ε

(1.9.1)

Свойство состоятельности может быть выражено двумя более жесткими требованиями, которые являются достаточными условиями состоятельности и которые легче поддаются практической проверке:

и (1.9.2)

2) Свойство несмещенности означает, что при любом конечном объеме выборки п

центр рассеяния статистики θ (математическое ожидание случайной величины θ) совпадает со значением оцениваемого параметра генеральной совокупности:

М(θ) = ξ — для любого п. (1.9.3)

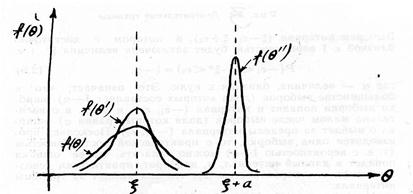
Естественно, что при заданном конечном объеме выборки п из различных возможных статистик для оценки параметра ξ следует выбрать ту статистику, которая, являясь несмещенной, обладает в то же время минимальным рассеянием, т.е. имеет минимальную дисперсию. Последнее свойство получило название эффективности.

Другие материалы:

Макет анкеты (опросника)
Общий вид и структура анкеты (опросника) не менее важны, чем содержание и словесное оформление вопросов. Плохое оформление или неясные инструкции часто ведут к невосполнимым пропускам в данных. Общая рекомендация, равно применимая и к во ...

Международное движение за права инвалидов. Зарубежный опыт
В социальной практике идея равенства прав граждан начала широко реализовываться только в XX столетии и, прежде всего, через защиту равных с другими прав для отдельных слоев общества[18]. Общество не сразу осознало, что нет смысла в демок ...

Институты власти как тормоз экономического развития. Институт власти-собственности
По мнению Д. Норта, для политических систем характерно производство неэффективных прав собственности, которые приводят к экономическому упадку. Автор выделяет две основные причины этого феномена. Во-первых, доходы, которые получают власть ...