SocioDone

Осталось привести лишь частные случаи. При a=0 имеем

I(F)=,

при a=1 получается мера расслоения Тайла (Theil):

I(F)=,

наконец, при a=2 имеем квадрат коэффициента вариации:

I(F)=,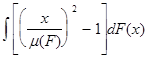

множители перед интегралом опущены в соответствии с определением разложимости.

Рассмотрим общество, заданное функцией распределения F, состоящее из m групп, каждая из которых определяется своей функцией распределения Fi (). В этом случае F=, где li³0, и Sli=1. Кроме того, чтобы F была функцией распределения всего общества необходимо представление распределения центров групп в виде F0(x)=SiH(x-xi)li, где H(x) - функция Хевисайда, т.е. она равна 1 при x³0 и 0 в других случаях, а li=ni/n и xi=m(Fi).

Остается привести лишь разложения уже приведенных показателей расслоения.

Для первого показателя - логарифмической меры расслоения - имеем функцию w(x)=-ln[x/m(F)], которая дает название меры. Для нее весовая функция p имеет вид p[m(Fi)]=1. а показатель расслоения

I[m(F)]=,

или, в более общем виде для распределения F(x)=, где F(x/l)=Fi(x) при l=m(Fi),

.

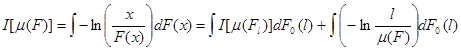Для меры неравенства Тейла функция w(x)=[x/m(F)]ln[x/m(F)], весовая функция p[m(Fl)]=[l/m(F)], поэтому,

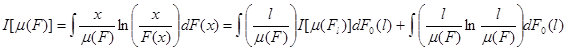
Для квадрата коэффициента вариации функция w(x)=[x/m(F)]2-1, весовая функция p[m(Fl)]=[l/m(F)]2 и

.

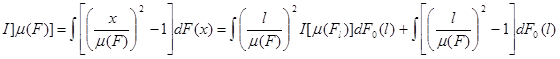В самом общем виде для функции w(x)=[x/m(F)]a-1 весовая функция p[m(Fl)] будет равна [l/m(F)]a, а разложимый показатель расслоения для любого a имеет вид

.

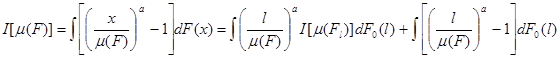Для того, чтобы убедиться в неотрицательности любого из приведенных показателей бедности следует проделать следующее. Во-первых, все представленные в показателях расслоения весовые функции w(x) выпуклы. Во-вторых, все функции распределения Fl таковы, что их средние значения равны единице. В-третьих, для выпуклых функций w справедливо неравенство Йенсена E

w(X)³w(E

X). Теперь, применив неравенство Йенсена к весовой функции w[x/m(F)] получаем требуемый результат.

Последнее обстоятельство, на которое необходимо обратить внимание, заключается в том, что функция Лоренца разложима в смысле уже данного определения. Действительно, пусть F(w)=SlIFi(w). Тогда справедливо равенство L(w)=(1|W)SliWiLi(w), которое следует из определения функции Лоренца после вынесения из-под знака интеграла Sli и умножения каждого слагаемого на Wi/Wi. Легко убедиться, что сумма весов (lIWi/W) последнего соотношения равна 1. Однако коэффициент Джини неразложим. Наконец, энтропия распределения, представляющего собой функцию Лоренца, это разложимая мера расслоения Тейла.

Другие материалы:

Семья как социальный институт
Семьей называется основанное на кровном родстве, браке или усыновлении объединение людей, связанных общностью быта и взаимной ответственностью за воспитание детей; члены семьи часто живут в одном доме. В США это определение включает множе ...

Содержание работы социального педагога в образовательном учреждении
Содержание работы социального педагога в соответствии с квалификационной характеристикой определяется ее педагогической направленностью. Это означает, что вся его профессиональная деятельность по сути представляет собой комплекс мероприят ...

Как интерпретирует социальное поведение разработанная Дж. Хомансом социологическая теория обмена?
Большое внимание исследованию социального поведения уделяется в социологической теории обмена, одним из основных авторов которой является американский социолог и социальный психолог Дж. Хоманс. Исходной единицей социологического анализа Х ...