SocioDone

Условие разложимости - это определение разложимого функционала J: функционал J называется разложимым, когда он, после подходящего монотонного преобразования, может быть представлена в виде уже приведенной суммы, где F0 - смесь функций распределения Fi в группах. В этом определении сразу дано такое представление функции J, которое могло бы быть дано в два этапа, первый - определение разложимости как некоторой зависимости от функций распределения в группах и на их центрах, и второй - приведение к аддитивной зависимости после монотонного преобразования. Если далее определить показатель (или меру) расслоения (или неравенства) I как разложимый функционал J, удовлетворяющую условиям 1-7, то может быть доказана следующая теорема.

Теорема

. Непрерывно дважды дифференцируемая разложимая мера расслоения удовлетворяет условиям передачи и однородности тогда и только тогда, кода она имеет вид

для некоторого a³0, где m(F) - центр распределения F, а wa(x) - решение уравнения x(d2w(x)/dx2)+(1-a)(dw/dx)=b.

Если учесть, что решения w(x) дифференциального уравнения xw”+(1-a)w’=b и соответствующие им p(Fl) имеют вид

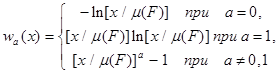и pa(Fl)=[l/m(F)]a,

то общим видом показателя расслоения будет следующий

.

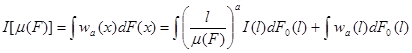Смешивающая функция для дискретных величин F0(l) в точке l=m(Fi) имеет скачёк величины li, для непрерывного случая аналогично.

Результат теоремы состоит, во-первых, в том, что мера расслоения не зависит от численности общества (или групп), а зависит лишь от функции распределения. Во-вторых, характеристических (существенных) свойств всего два - однородности и передачи.

Все остальные следуют из них. Таким образом, не было необходимости приводить и описывать все свойства расслоения, хотя они многое проясняют. Более того теорема показывает, что меру расслоения можно искать в виде и функция w(x) связана с множеством решений уравнения xw”(x)+(1-a)w’(x)=b.

Другие материалы:

Рентабельность образования. Альтернативные потоки заработков
Рентабельность чел. капитала исчисляется путем отнесения дохода от него к его стоимости. Норма отдачи измеряет степень эф-ти инвестиций. Отдача от вложения в чел-ка в среднем много выше, чем от вложений в физ.капитал. Однако в случае чел. ...

Современный уровень жизни населения. Снижение уровня жизни
Оно происходило в течение всего периода постсоветских рыночных реформ. Индекс развития человеческого потенциала снизился с 0,848 в 1992г. до 0,78 в 1996г.; по этому показателю Россия была отброшена в число развивающихся стран. За годы ре ...

Система категорий социологического исследования семьи
Развитие любой области научного знания неразрывно связано с уточнением и совершенствованием языка науки. Четкий и научно обоснованный понятийный аппарат является важным средством институционализации и формализации науки, создания предпосы ...